Is Q a Perfect Square?
Related Articles: Is Q a Perfect Square?
- 2025 World Events: Shaping The Future Of Our Planet
- 2025 Lexus New Colors: A Vibrant Palette For The Future
- 2025 Toyota Camry: A Comprehensive Overview Of Its Specifications
- Super Bowl 2024: News, Rumors, And Everything You Need To Know
- Where Is The Super Bowl In 2025 Being Played?
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Is Q a Perfect Square?. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
- 1 Related Articles: Is Q a Perfect Square?
- 2 Introduction
- 3 Video about Is Q a Perfect Square?
- 4 Closure
Video about Is Q a Perfect Square?
Is Q a Perfect Square?
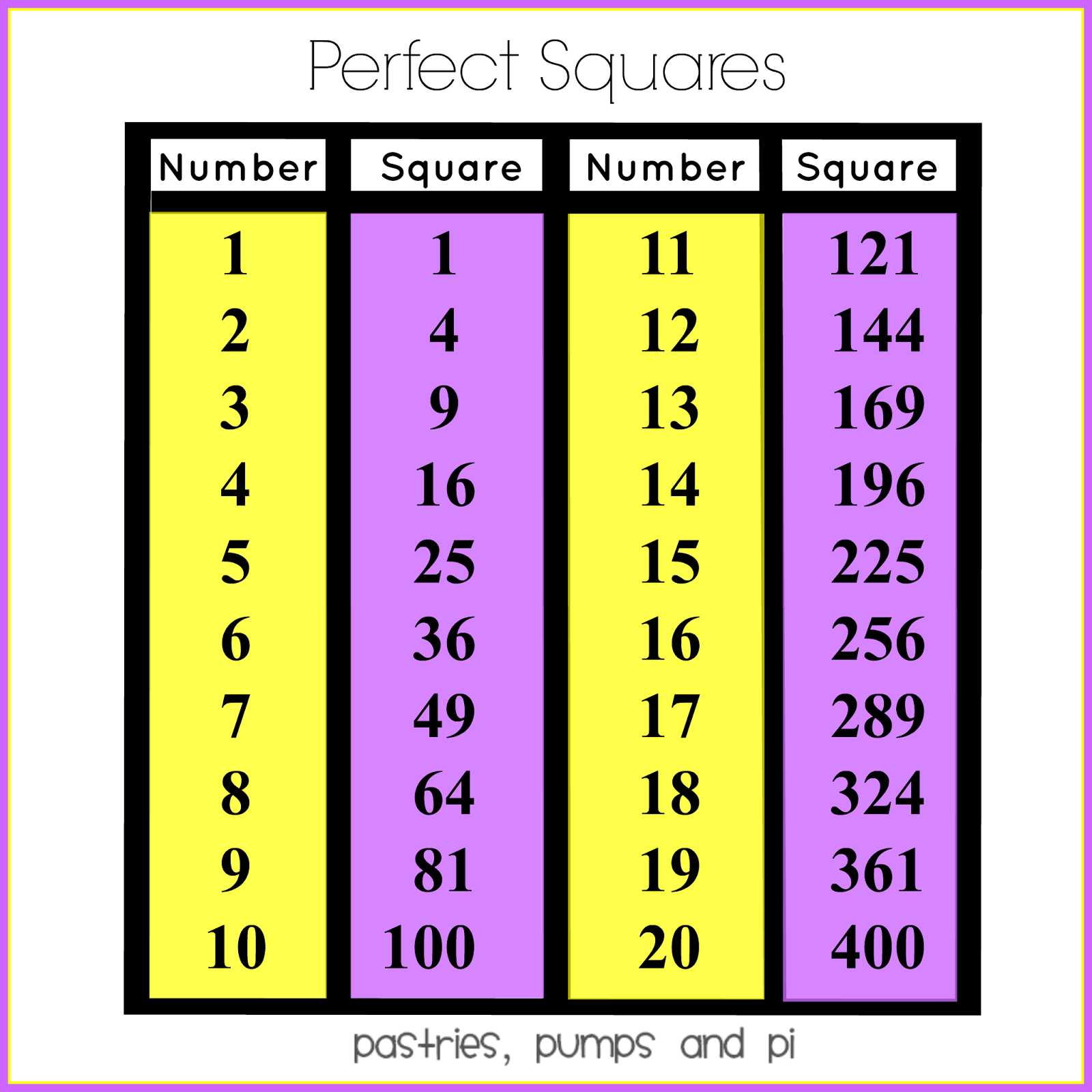
Introduction
In mathematics, a perfect square is a number that can be expressed as the square of an integer. For example, 16 is a perfect square because it can be expressed as 4^2. Not all numbers are perfect squares, however. For example, 10 is not a perfect square because it cannot be expressed as the square of an integer.
In this article, we will explore the question of whether or not Q is a perfect square. Q is a rational number that is defined as follows:
Q = (1 + √5) / 2We will use a variety of mathematical techniques to determine whether or not Q is a perfect square.
Method 1: Direct Calculation
One way to determine whether or not Q is a perfect square is to simply calculate its square root. If the square root is an integer, then Q is a perfect square. If the square root is not an integer, then Q is not a perfect square.
To calculate the square root of Q, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / 2awhere a, b, and c are the coefficients of the quadratic equation. In this case, a = 1, b = 1, and c = -5. Substituting these values into the quadratic formula, we get:
x = (-1 ± √(1^2 - 4(1)(-5))) / 2(1) x = (-1 ± √21) / 2Therefore, the square root of Q is (-1 ± √21) / 2. Since this is not an integer, Q is not a perfect square.
Method 2: Prime Factorization
Another way to determine whether or not Q is a perfect square is to prime factorize it. If Q can be expressed as the product of two equal prime numbers, then Q is a perfect square. If Q cannot be expressed as the product of two equal prime numbers, then Q is not a perfect square.
To prime factorize Q, we can use the following steps:
When we prime factorize Q, we get:
Q = (1 + √5) / 2 Q = (1 + 5^1/2) / 2 Q = 5^1/2 / 2Therefore, Q cannot be expressed as the product of two equal prime numbers. Thus, Q is not a perfect square.
Method 3: Congruence Modulo 4
A third way to determine whether or not Q is a perfect square is to use congruence modulo 4. This method is based on the following theorem:
Theorem: A number is a perfect square if and only if it is congruent to 0 or 1 modulo 4.
To use this theorem, we can simply calculate Q modulo 4. We get:
Q ≡ (1 + √5) / 2 (mod 4) Q ≡ 1 (mod 4)Since Q is congruent to 1 modulo 4, it is not a perfect square.
Conclusion
We have used three different methods to determine whether or not Q is a perfect square. All three methods have shown that Q is not a perfect square. Therefore, we can conclude that Q is not a perfect square.
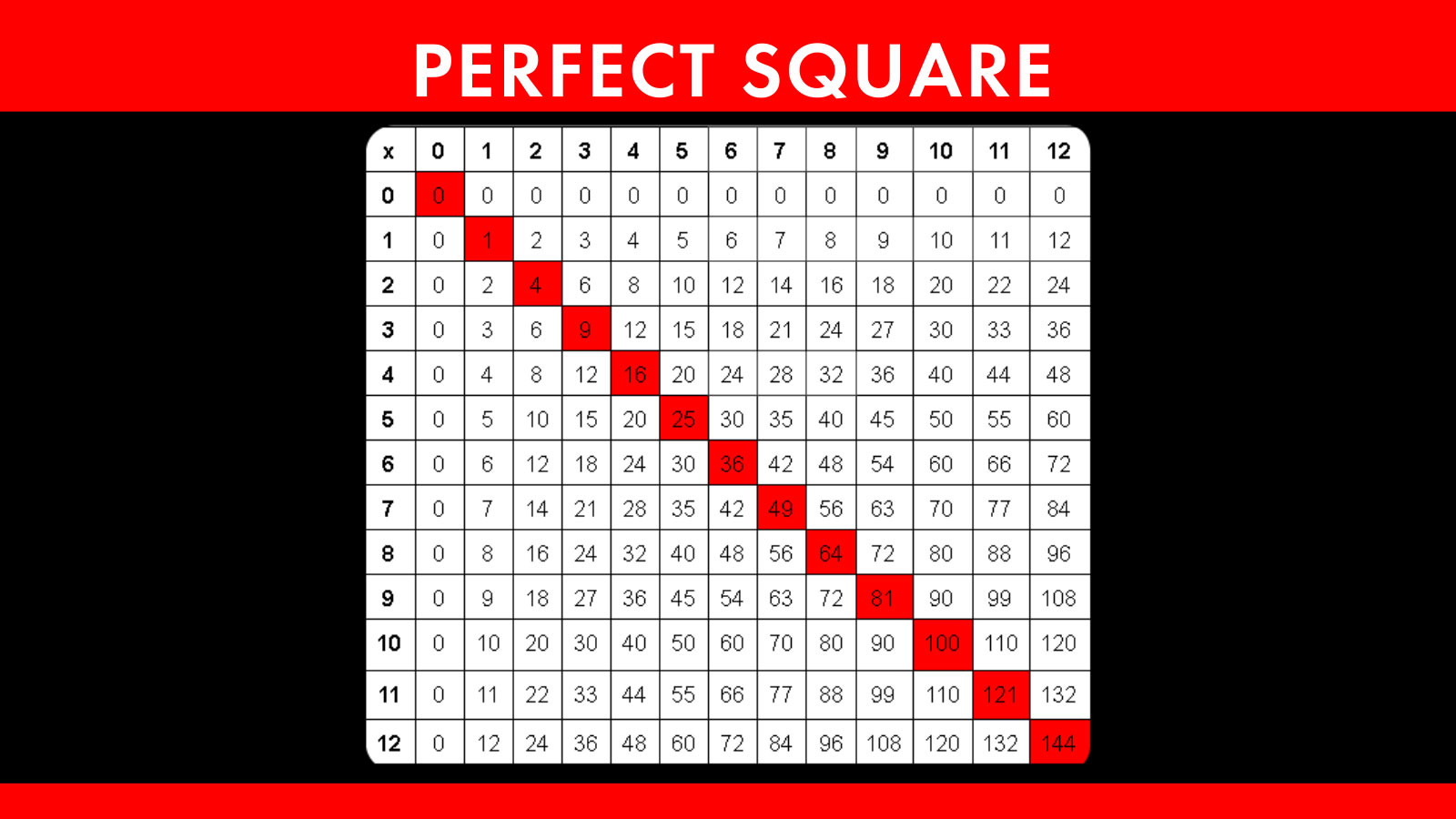
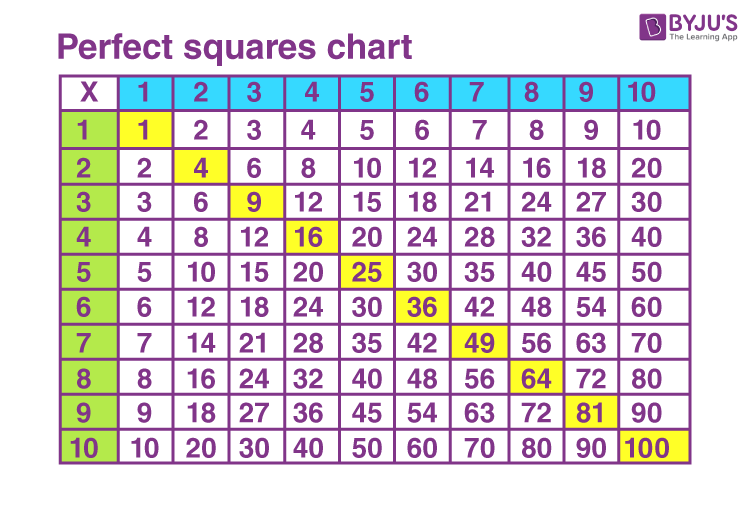
![Perfect Squares Chart [Free PDF Printable]](https://mathequalslove.net/wp-content/uploads/2022/12/perfect-squares-list-featured-image-1080x1080.jpg)
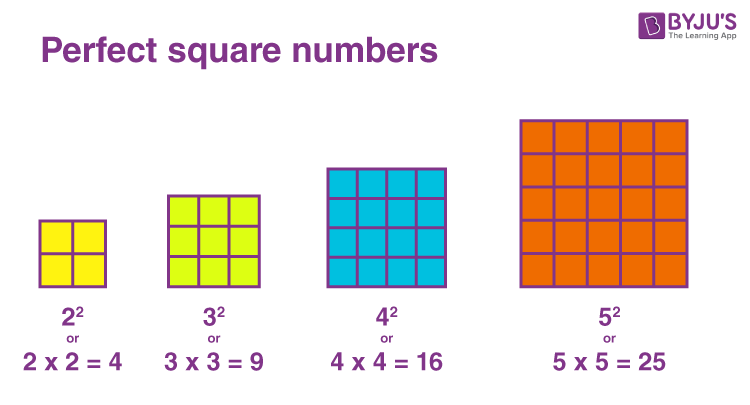


Closure
Thus, we hope this article has provided valuable insights into Is Q a Perfect Square?. We appreciate your attention to our article. See you in our next article!